- 機器學習簡介
- 線性模型(迴歸分析)
- Regularization
- Support Vector Machine
- 分類樹
- Bagging 與 Random Forest
- Boosting 與 Gradient Boosted Decision Tree
- Neuron Network
Machine Learning
Wush Wu
國立台灣大學
課程大綱
機器學習簡介
什麼是學習
- 字典定義:因為知識、教育、研究或經驗而改變行為
- 機器學習:讓機器具備學習能力的技術
人工智慧
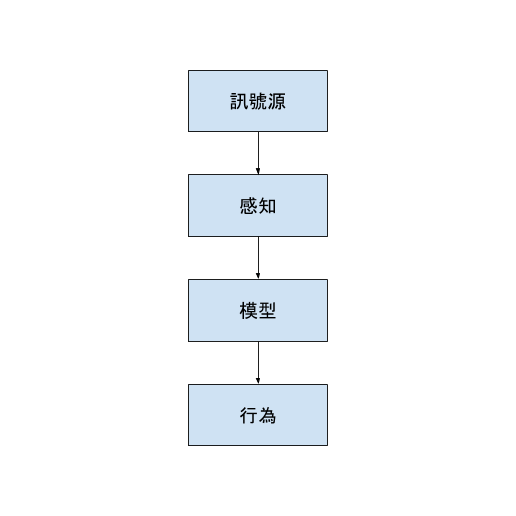
廣告播放的自動化系統
- 訊號源:使用者的瀏覽特定的網站
- 感知:使用者的特性、網站的特性
- 模型:男生喜歡電玩相關廣告、女生喜歡化妝品相關廣告
- 行為:猜測使用者的性別。如果可能是男生,就播放電玩相關廣告;如果可能是女生,就播放化妝品相關廣告
機器學習
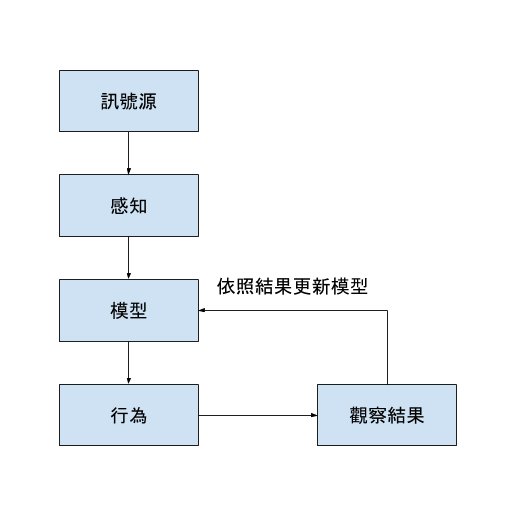
廣告播放的自動化學習系統
- 訊號源:使用者的瀏覽特定的網站
- 感知:使用者的特性、網站的特性
- 模型:男生喜歡電玩相關廣告、女生喜歡化妝品相關廣告
- 行為:猜測使用者的性別。如果可能是男生,就播放電玩相關廣告;如果可能是女生,就播放化妝品相關廣告
- 學習:依照播放的結果,調整電玩廣告和化妝品廣告的比例
課堂中的機器學習
為什麼我們要讓機器去學習?
- 機器學習不能解決所有的問題
- 問題必須要轉換成機器學習可以解決的問題
- 機器學習系統需要成本做開發
- 機器學習系統需要額外的維護成本(http://www.slideshare.net/WushWu/ss-55964136)
- 機會成本:如果一開始能讓機器把任務做好,何必讓它花時間學習?
實際的問題 \(\Rightarrow\) 機器學習問題
- 機器學習能解決的問題:
- 預測數值
- 分類
- 我們想要增加廣告的營收
- 廣告的營收和點擊率相關
- 在每次推播廣告給瀏覽者前,考慮「該瀏覽者點擊每種廣告的機率」
- 預測瀏覽者點擊每種廣告的機率
實際的問題 \(\Rightarrow\) 機器學習問題
- 我們想要了解詞彙的結構
- 利用每個詞彙前後的詞彙,來預測各個詞彙的機率
使用機器學習的好處
人的主流意見可能出錯
- 範例:
- 我們以為女生不喜歡遊戲類廣告
- 有些手機遊戲是針對女生設計
「模型」可能複雜到人無法處理
- \(Y = f(X)\) 的 \(f\) 可能複雜到人無法一開始就設計出好的答案
- 範例:
- 瀏覽者有數十種標籤
- 有數百個網站與廣告
環境的特性一直在改變
- 人無法跟上環境的改變
- 範例:
- 簽約的網站與廣告會一直更換
- 瀏覽者的喜好也會一直更換
我們該使用機器學習相關技術嗎?
- 人可以做嗎?
- 使用機器學習的成本 v.s. 使用人的成本
- 範例:decaptcha
Captcha
- 用於分辨人或電腦的問題
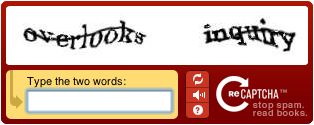
Decaptcha
- 想要用電腦做某些事情時,必須要讓電腦能通過Captcha
- Decaptcha的方式:
- 影像辨識
- 群眾外包 https://anti-captcha.com
你真的需要使用機器學習嗎?
- 你的問題可以轉換成機器學習能解決的問題嗎?
- 你的問題用人解決很昂貴,或是不可能嗎?
- 你有維護機器學習解決方案的人嗎?
研究機器學習時的常用名詞
- $Y$:目標變數、應變變數、response
- $X$:解釋變數、獨立變數、covariates
機器學習解決的問題
- 監督式學習:給定 \(X\) ,預測 \(Y\)
- 分類: \(Y\) 是類別型變數
- 迴歸: \(Y\) 是解釋型變數
- 非監督式學習:給 $X$,對 \(X\) 分群
分類問題(\(Y\) 是類別型變數)
- 二元分類
- 點擊預測: \(Y =\) 使用者會不會點廣告
- 股票的漲跌: \(Y =\) 下一個單位時間股價會往上走或往下走
- 多元分類
- 手寫辨識: \(Y =\) 使用者所撰寫的字
- 語音辨識: \(Y =\) 使用者所發出的聲音
回歸問題($Y$是連續型變數)
- 股價預測 :\(Y =\) 下一個單位時間時,特定股票的股價
- 物價預測 :\(Y =\) 特定商品在下一個單位時間的價格
叢集問題($Y$不存在)
- 顧客分群: \(X =\) 顧客的特徵
- 廣告分群: \(X =\) 廣告的特徵
機器學習技術較常用應用於預測
- 預測型分析
- 在事件發生之前,預測事件的結果
- 利用預測結果,決定動作
預測型分析的特性
- 模型的準確度是主要目的
- 不在乎模型的內容是否能帶來知識
- 通常預測精準的模型,都會複雜到人類難以理解(黑盒子)

解釋型分析
- 挖掘現象的因果關係
公司的營收
- 預測明年公司營收的準確度價值不高
- 9~10億 \(\Rightarrow\) 9.9億~10.1億
- 找出影響公司營收的原因價值很高
解釋型分析的特性
- 模型的合理性是主要目的
- 模型通常不準
- 分析師必須要能夠透過模型尋找出價值
- 例:透過分析資安數據,發現特定作業系統比較脆弱,容易發生資安事件
機器學習的原理
機器如何學習
- 相信過去的資料能夠代表未來
- 找到代表過去的特徵
- 該特徵會維持到未來
- 「資料具有代表性」
請同學預測六年甲班的數學考試的平均成績
- 請選擇:
- 10分
- 50分
- 100分
- 200分
請同學預測六年甲班的數學考試的平均成績
- 已知上次考試中,四位同學的成績是:220, 240, 235, 225
- 請選擇
- 10分
- 50分
- 100分
- 200分
機器如何學習
- 相信過去的資料能夠代表未來
- 找到代表過去的特徵
- 該特徵會維持到未來
- 「資料具有代表性」
代表性很重要
- 如果六年甲班許多同學不同
- 如果上次的出題老師與這次的出題老師不同
- 如果上次的數學考試滿分為240, 這次的滿分為1000
機器如何學習
- 尋找訊號
- 評分(Loss Function)
- 優化
評分 ==> 預測
- 四位同學的成績是:220, 240, 235, 225
- 定義:「準」
- 可依據各種距離公式定義「準」
- 我們計算差距的平方和作為Loss(越低越好)
- 請選擇
- 10分 (Loss: 193850)
- 50分 (Loss: 129850)
- 100分 (Loss: 67850)
- 200分 (Loss: 3850)
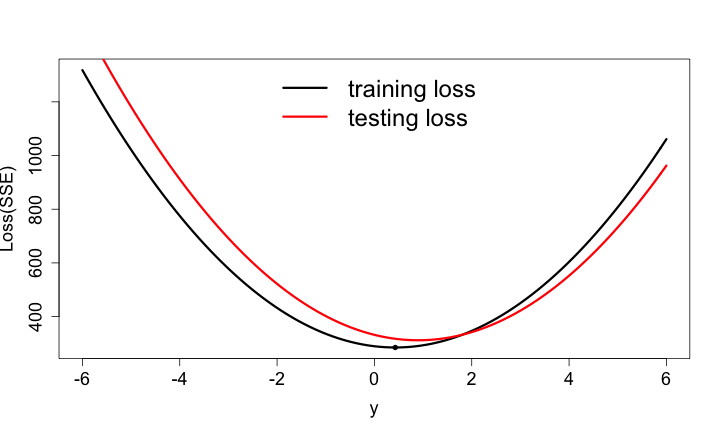
評分 ==> 優化 ==> 預測
- 四位同學的成績是:220, 240, 235, 225
- 我們計算差距的平方和作為Loss
- 猜230分的loss最小 (250)
這種方法的預測結果真的會好嗎?
- 如果六年甲班許多同學不同
- 如果上次的出題老師與這次的出題老師不同
- 如果上次的數學考試滿分為240, 這次的滿分為1000
...
這種方法的預測結果真的會好嗎?
- 「假設」數學考試的分數出自常態分佈
- 該常態分佈的中心點是未知的
- 看到四個樣本點:\(x_1, x_2, x_3, x_4\)
- 研究若干個樣本點與中心點的數學性質:
- 如果有$n$個點:\(x_1, ..., x_n\)
- \(n\) 個觀測點的平均 \(\bar{x}_n\)
- 當\(n\) 趨近於無限大: $\bar{x}_n$會收斂到中心點
- 差距大約和$\sqrt{n}$成反比
不同學科對這個問題的看法不同
- 統計:假設 ==> 推導數學性質 ==> 會收斂 ==> 收斂速度
- 資訊:評分 ==> 優化 ==> 實驗實驗實驗
預測的原理
範例
- \(y = 3 tan^{-1}(5 x) + z + \varepsilon\)
- \(\varepsilon \sim N(0, 0.01)\)
| y | x | z |
|---|---|---|
| -3.449232 | -0.6264538 | 0.3981059 |
| 1.620552 | 0.1836433 | -0.6120264 |
| -3.757597 | -0.8356286 | 0.3411197 |
| 3.224672 | 1.5952808 | -1.1293631 |
| 4.443377 | 0.3295078 | 1.4330237 |
| -1.837960 | -0.8204684 | 1.9803999 |
| 3.248735 | 0.4874291 | -0.3672215 |
| 2.965666 | 0.7383247 | -1.0441346 |
| 4.317580 | 0.5757814 | 0.5697196 |
| -2.939782 | -0.3053884 | -0.1350546 |
只有觀察y
機器學習的原理 - 看到x與y
看到x與y
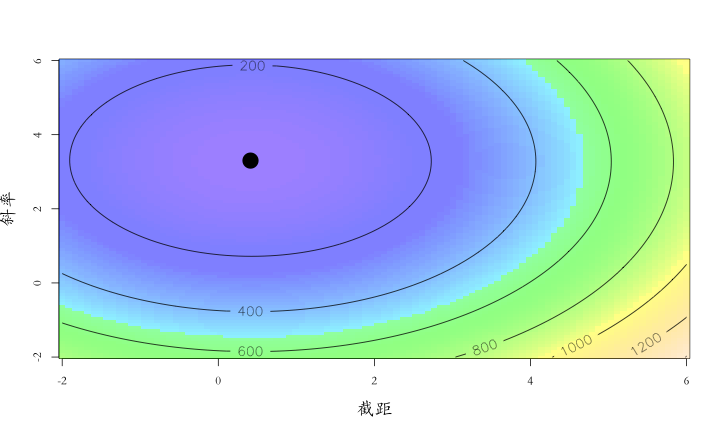
優化
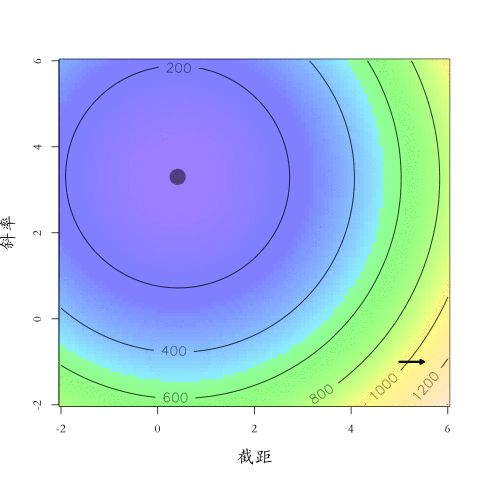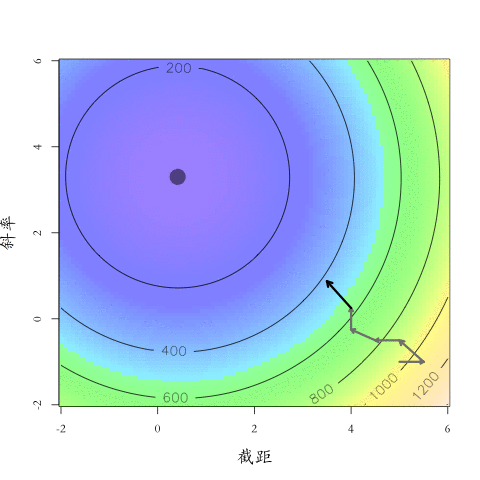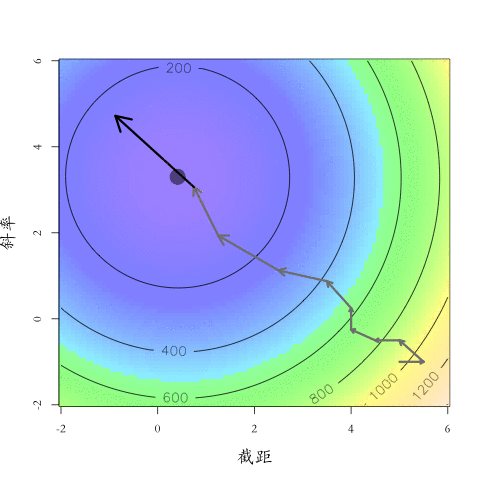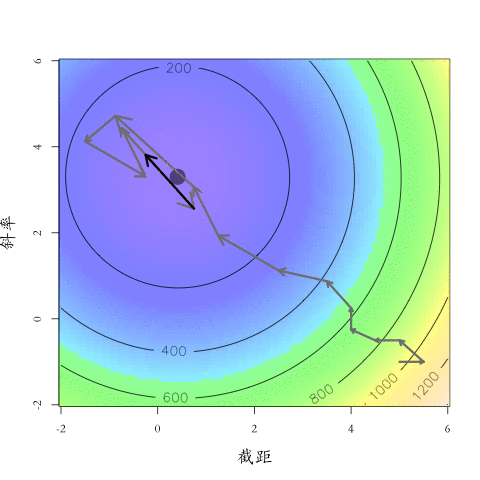
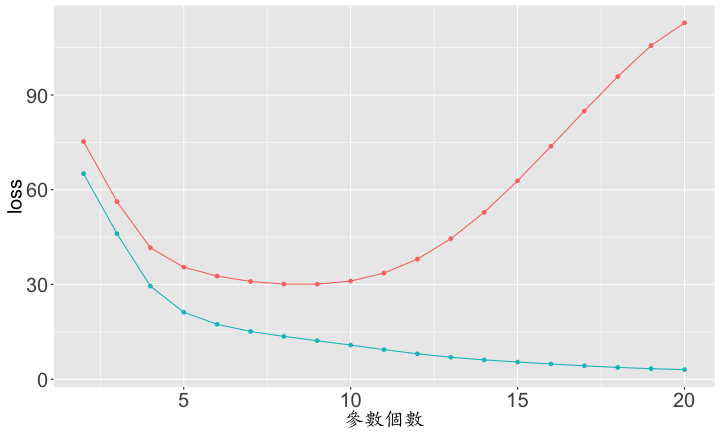
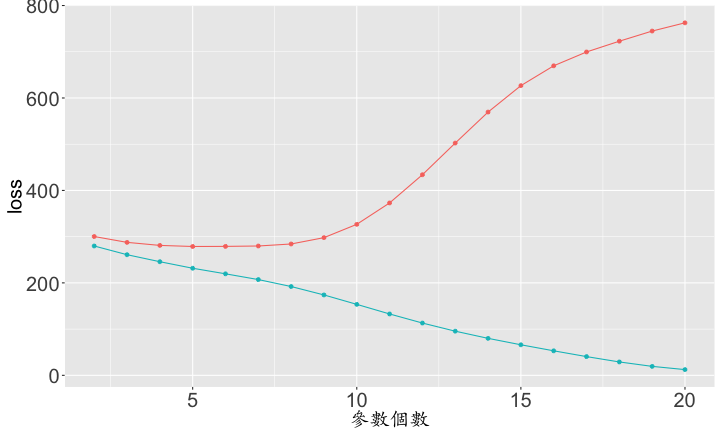
大「量」數據的機器學習挑戰:優化
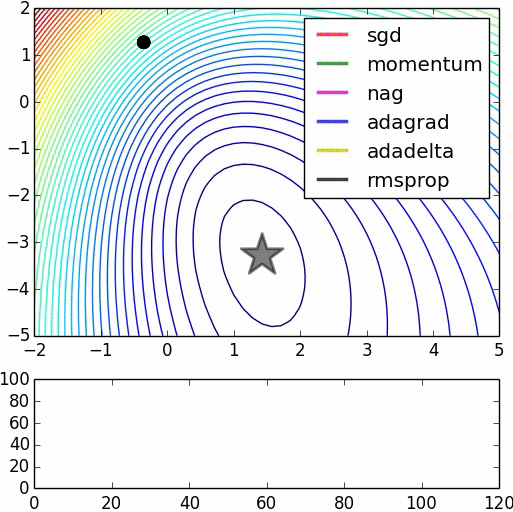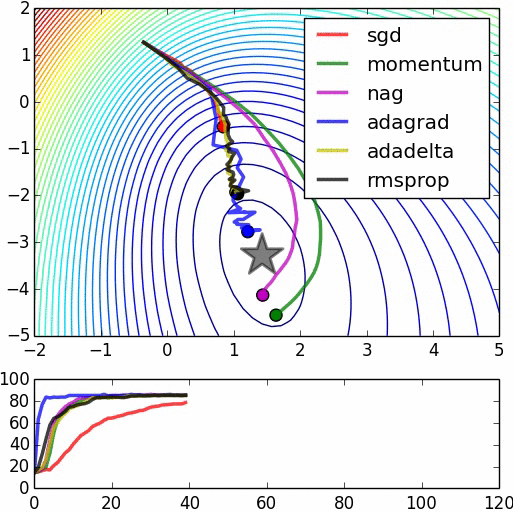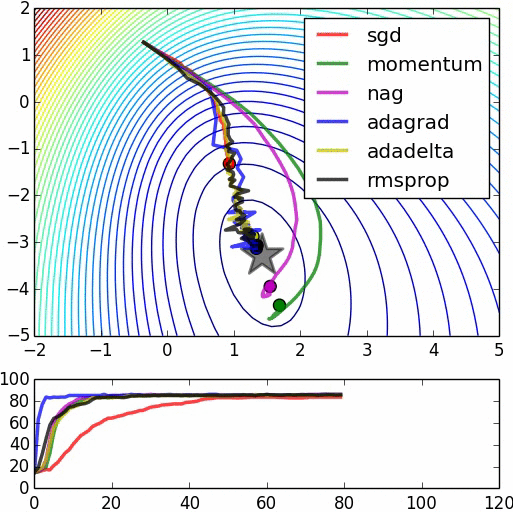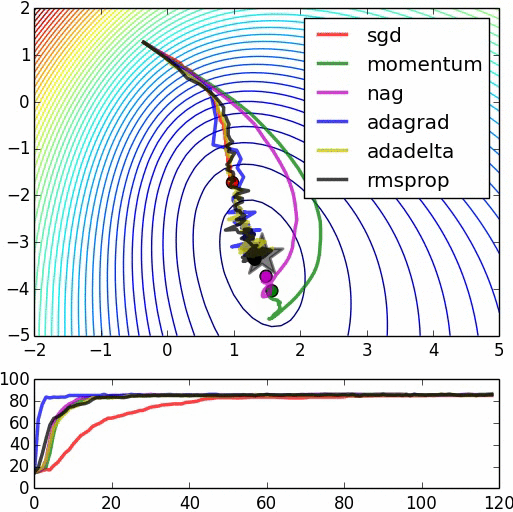
Testing Dataset的Loss
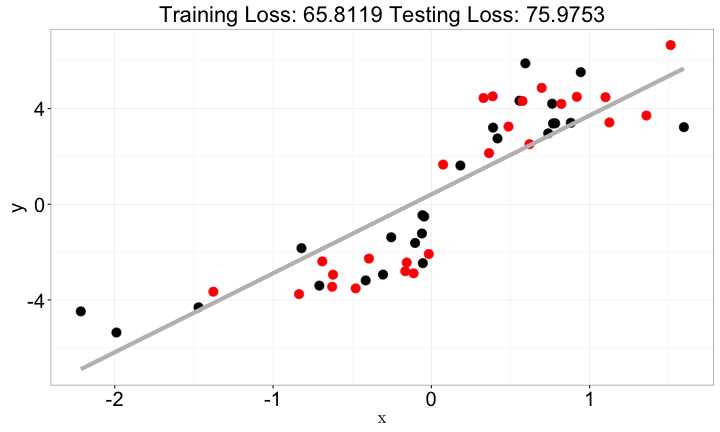
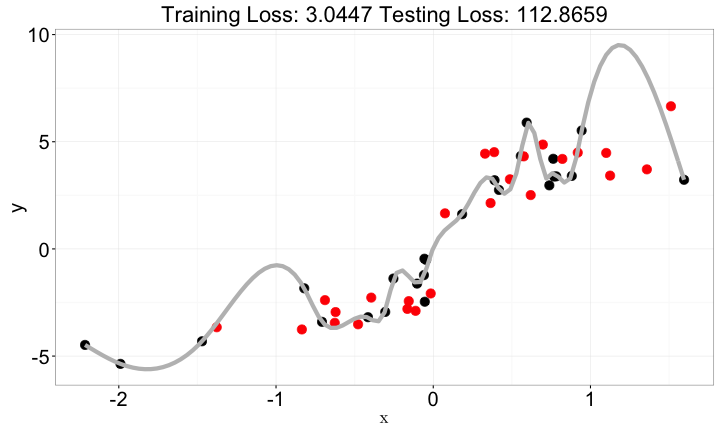
複雜化x與y的關係
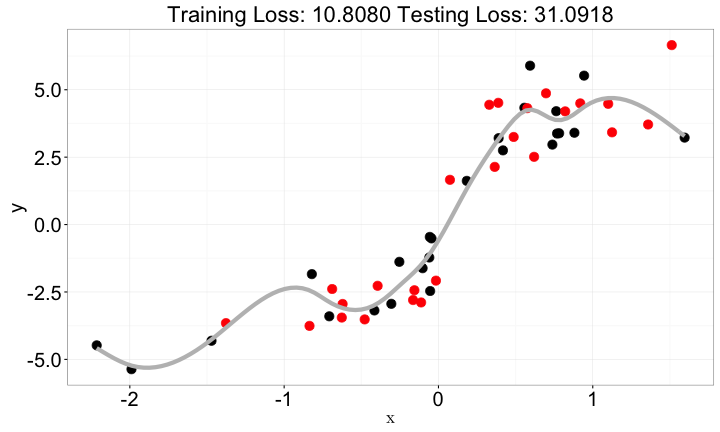
複雜化x與y的關係
複雜化x與y的關係
從y到x與y
- 只有
y=> 用常數做預測 - 有
x與y=> 用f(x)做預測f越複雜,結果不一定越好- 通常是一個開口向上的曲線
f(x)如果不夠複雜:lack of fitf(x)如果過度複雜:overfitting
z與y
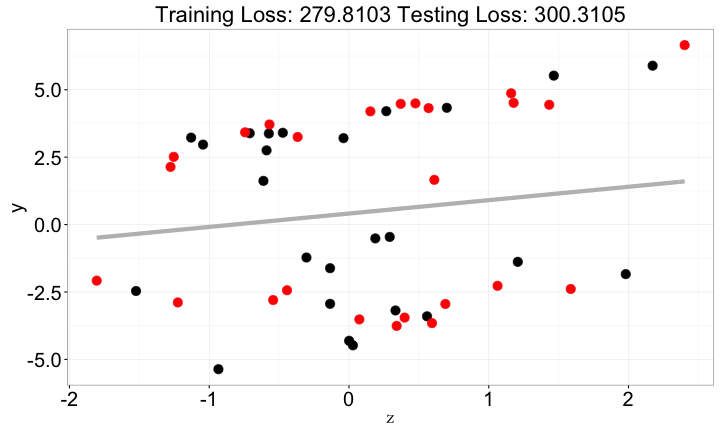
z與y
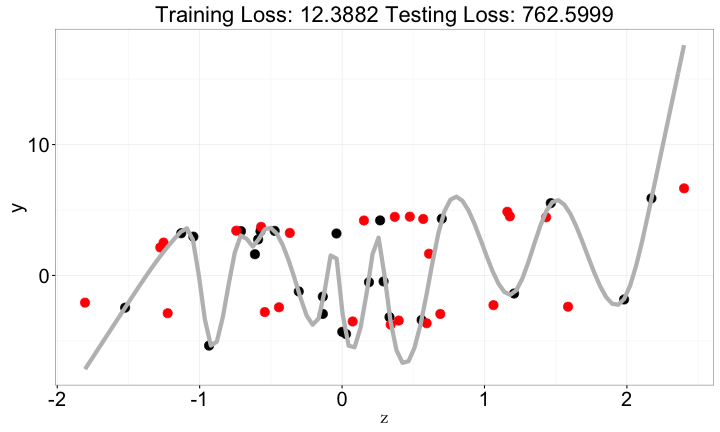
y => z與y
- 單獨看
z並沒有包含太多y的資訊- 從
zv.s.y的圖可以看出
- 從
x、z與y
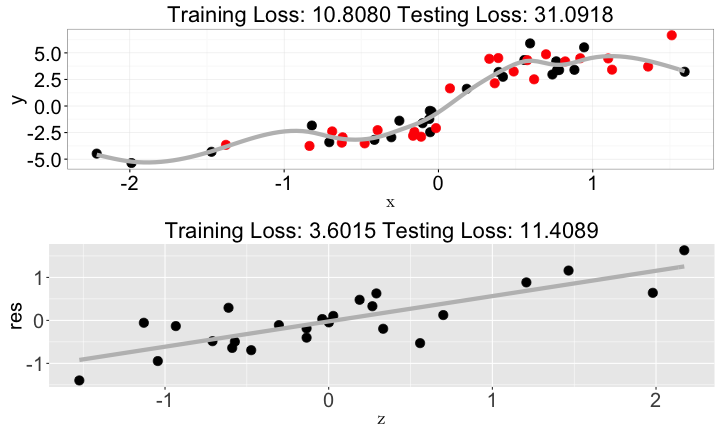
如何做出好模型?
- 模型要複雜又不能太複雜
- 可利用training / testing dataset來抓
- 找到有資訊的相依變數
- x-y plot可以檢查單一解釋變數與目標變數的關係
- x-y plot無法檢查多變數間的交互關係
- 尋找相依變數是藝術
線性模型(迴歸分析)
統計模型
- $Y$是我們感興趣的變數, $X$是可能跟$Y$相關的資料
- 當$Y$未知時,$X$仍已知
- \(Y = f(X) + \varepsilon\)
- $f(X)$描述我們理解的變化,使用的數學不牽涉到機率
- \(\varepsilon\) 描述我們不能理解的變化,通常 \(\varepsilon\) 是隨機變數,使用的數學需要機率
有沒有$\varepsilon$的差別
- \(Y = f(X)\):
- 只有描述我們對Y的期待值
- 對於隨機性質沒有描述
- \(Y = f(X) + \varepsilon\)
- 我們會假設$\varepsilon$的機率性質
- 一旦取得$\varepsilon$的分佈,即可找出估計$f$的方式,以及該方式估計$f$的特性
- 分佈:機率密度函數、幾率質量函數或是一群有代表性的樣本
統計與機器學習
- 評分的定法
線性模型
- \(Y\) 是煞車滑行的距離
- \(X\) 是車速
- \(Y = f(X) + \varepsilon\)
- \(f(X) = \beta_0 + \beta_1 X\)
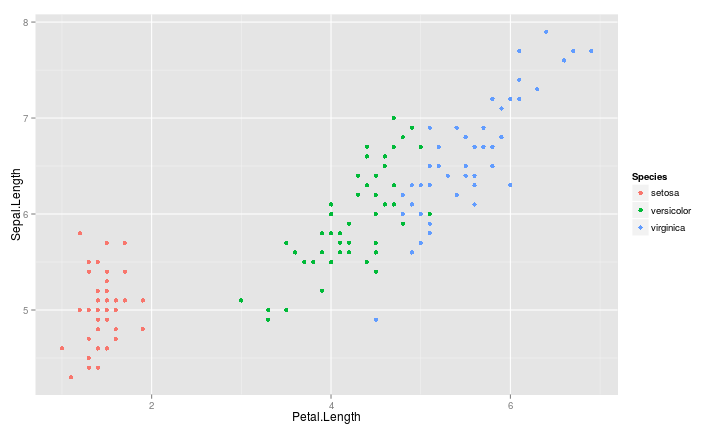
X-Y 散佈圖
- \((x_1, y_1), (x_2, y_2), ...\) :已知$X$推測\(Y\)
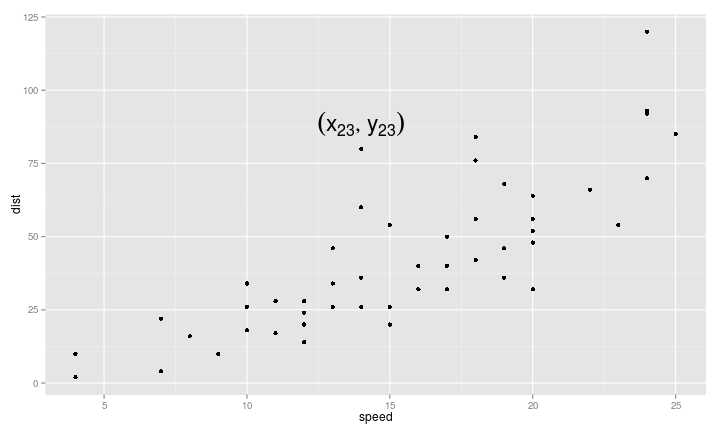
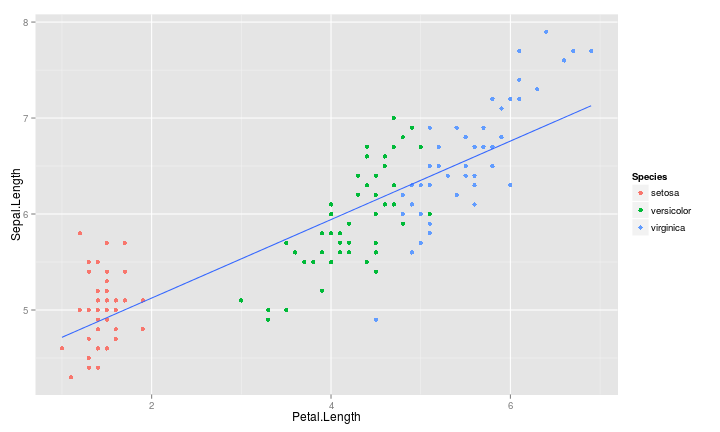
最小方差直線
- \(Y = \beta_0 + \beta_1 X\)
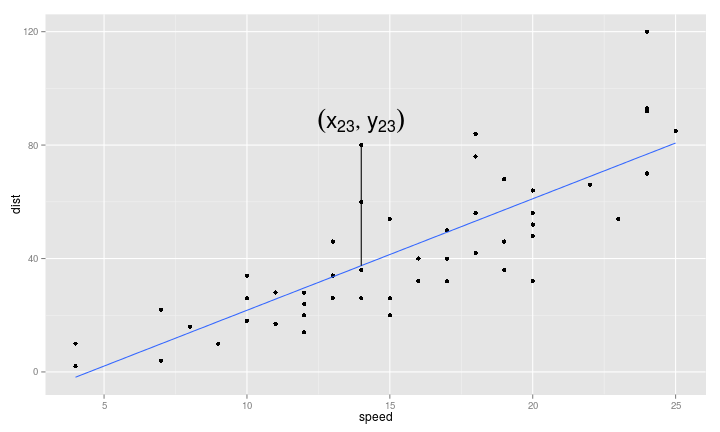
最小方差直線的性質
- \(Y = \beta_0 + \beta_1 X + \varepsilon, \varepsilon \overset{i.i.d.}{\sim} N(0, \sigma^2)\)
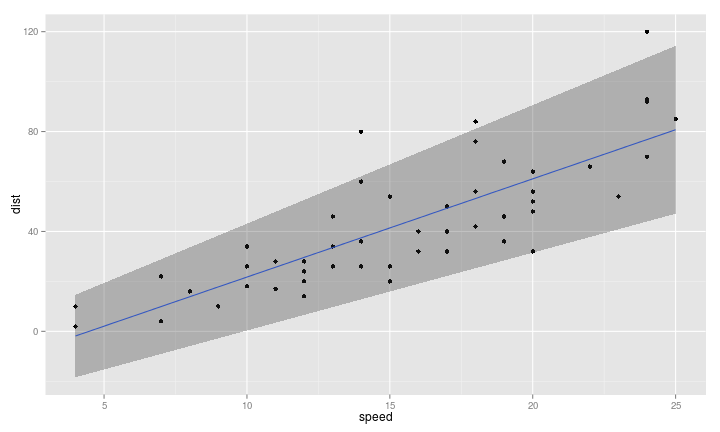
線性模型
- \(X\) 不一定只有一個變數,可能有: \(X_1, X_2, ..., X_p\)
- \(Y = \beta_0 + \sum_{i=1}^p \beta_p X_p\)
- 線性模型是「可以」解釋的
- Dist = -17.5790949 + 3.9324088 \(\times\) Speed + \(\varepsilon\)
- \(\varepsilon \overset{i.i.d.}{\sim} N(0, 236.5316886)\)
線性模型
- 線性模型是非常泛用的模型
- 具備有豐富的彈性
- 具備有良好的解釋性
- 可以透過「交互作用」產生複雜的模型
- 統計學家對線性模型的理解非常深入: 當 \(\varepsilon \overset{i.i.d.}{\sim} N(0, \sigma^2)\)
- 知道最好的估計方法:最小方差直線
- 知道$\varepsilon$對估計方法的影響
線性模型的範例
| Dependent variable: | |
| dist | |
| speed | 3.932*** |
| (0.416) | |
| Constant | -17.579** |
| (6.758) | |
| Observations | 50 |
| R2 | 0.651 |
| Adjusted R2 | 0.644 |
| Residual Std. Error | 15.380 (df = 48) |
| F Statistic | 89.567*** (df = 1; 48) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
線性模型,不只是直線
- 上述的最小方差直線,在 Speed = 0,預測的煞車距離為 -17.579
- 負的煞車距離不合理
- \(Y\) 都是正的,所以我們取log
線性模型,可以處理非直線的模型
- \(log(Y) = \beta_0 + \beta_1 X\)
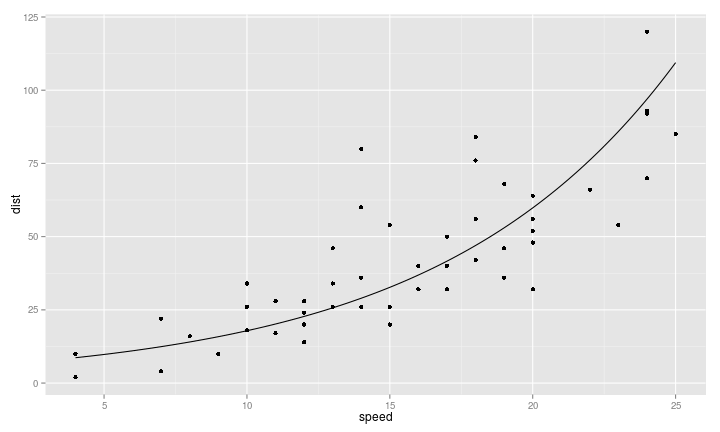
線性模型也可以解決二元分類問題
- \(Y =\) 煞車距離超過50; \(P(Y \text{ is TRUE}) = \frac{1}{1 + e^{\beta_0 + \beta_1 X}}\)
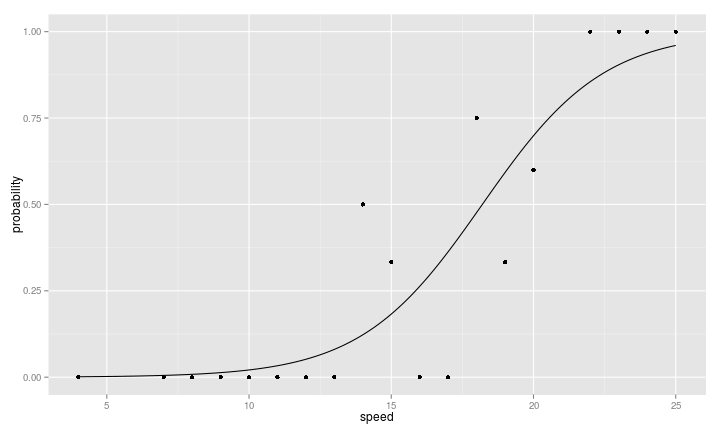
Logistic Regression
- $\beta_0 + \beta_1 X$:線性
- \(\frac{1}{1 + e^{\beta_0 + \beta_1 X}}\) :將實數線( \((-\infty, \infty)\) )轉換至 \((0, 1)\)
- \(\varepsilon\) 的地位由銅板機率( Bernoulli )取代
- 常用於許多領域:罕見疾病分析、廣告點擊率分析...
線性模型還有許多變形
- Poisson Regression:當資料為非負整數
- Isotonic regression:當資料嚴格遞增
\(X\) 的組合
- 要建立好的線性模型,$X$的挑選是很重要的
- $X$間的交互作用項與轉換是常用的技巧
- $X$設定很吃經驗、知識
交互作用
不考慮交互作用
考慮交互作用
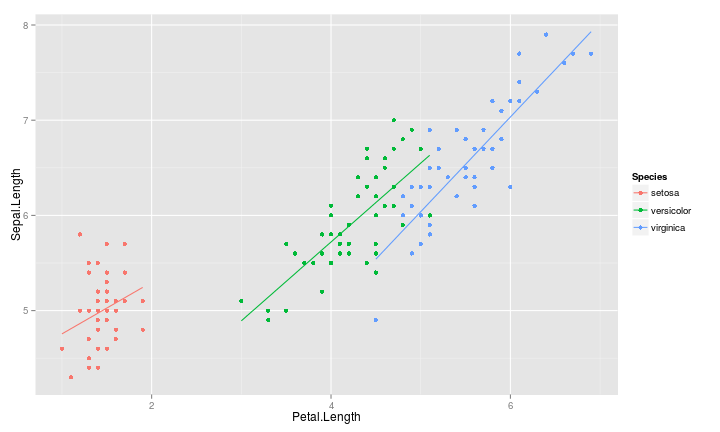
交互作用的應用:廣告推薦
- 推薦點擊率最高的廣告
- 廣告點擊率 = 廣告 + 網站
- 所有網站上的廣告播出順序都一致
- 廣告點擊率 = 廣告 * 網站
- 廣告的影響力會受到網站的影響
- 不同網站的廣告播出順序會不同
多種類別的分類
- 類別1 建立一個logistic regression model
- 類別2 建立一個logistic regression model
- 類別K-1 建立一個logistic regression model
- 類別 \(k \neq K\) 的機率為 \(\frac{e^{\beta_k^x}}{1 + \sum_{i=1}^{K-1} e^{\beta_i^x}}\)
- 類別 \(K\) 的機率為 \(\frac{1}{1 + \sum_{i=1}^{K-1} e^{\beta_i^x}}\)
多種類別的分類
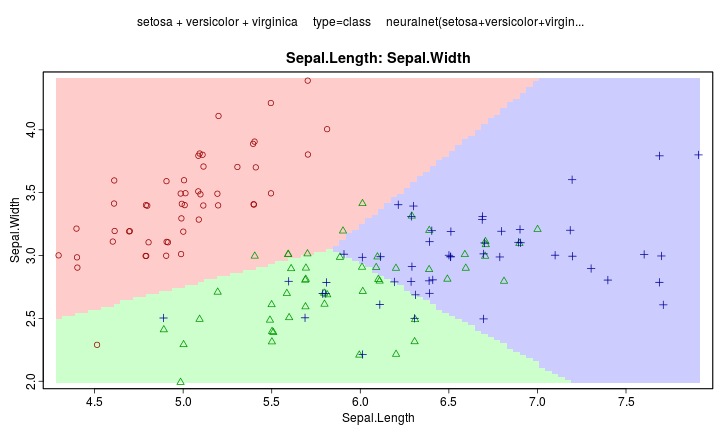
R 功能介紹:lm與glm
- 請同學完成:
Optional-RMachineLearning-01-Linear-Model - 請同學完成:
Optional-RMachineLearning-02-Generalized-Linear-Model
Regularization
金門縣年齡預測
- 我們有民國104年12月的全金門縣縣民的年齡資料

20名金門縣縣民的年齡樣本
- 由於有母體資料,可以一直產生新的「20名金門縣縣民樣本年齡樣本」:
[[1]]
[1] 25 32 46 67 22 66 74 51 49 7 22 20 52 33 57 41 54 87 33 57
[[2]]
[1] 72 22 50 17 26 33 1 33 63 30 39 47 40 21 60 51 58 15 54 35
[[3]]
[1] 60 50 57 44 43 58 2 39 55 52 39 62 37 24 9 14 29 42 51 34
母體平均數
- 40.452398
樣本平均數
[1] 25 32 46 67 22 66 74 51 49 7 22 20 52 33 57 41 54 87 33 57
=> [1] 44.75
[1] 72 22 50 17 26 33 1 33 63 30 39 47 40 21 60 51 58 15 54 35
=> [1] 38.35
[1] 60 50 57 44 43 58 2 39 55 52 39 62 37 24 9 14 29 42 51 34
=> [1] 40.05
[1] 68 27 38 30 50 25 39 56 11 63 30 61 31 30 39 65 63 33 57 77
=> [1] 44.65
[1] 36 54 34 29 56 22 53 17 24 18 24 7 50 63 57 58 38 35 59 48
=> [1] 39.1
[1] 50 31 26 88 49 22 18 39 70 47 81 55 31 36 19 1 54 14 37 50
=> [1] 40.9
[1] 87 40 40 20 56 38 42 22 23 47 46 10 3 50 71 47 45 43 84 41
=> [1] 42.75
[1] 52 47 24 25 55 37 20 55 15 63 48 45 30 37 41 21 43 10 26 22
=> [1] 35.8
樣本平均數的性質
- 樣本平均數也是隨機變數
- 樣本平均數常常被用來估計母體平均數
樣本平均數的分佈

樣本平均數的性質
- 平均值約:40.4446
- 母體平均值為:40.452398
- 變異數約:22.3723282
- 常用的「評分」:Mean Squared Error(MSE):\(Bias^2 + Variance\)
- (中心點準不準?)Bias:
樣本平均值 - 母體平均值 - (散佈大不大?)Variance:
樣本的變異數 - MSE: 22.372389
- (中心點準不準?)Bias:
估計量
- 只有20個金門縣縣民的年齡樣本,要猜測金門縣縣民的平均年齡
- 樣本平均數
- 樣本中位數
- 樣本平均數 * 0.99
估計量的MSE
- (
Bias^2 + Variance = MSE) - 樣本平均數:6.0808569 × 10-5 + 22.3723282 = 22.372389
- 樣本中位數:0.0025102 + 45.7815253 = 45.7840355
- 樣本平均數 * 0.99:0.1699451 + 21.9271188 = 22.0970639
偏差與散佈程度
- 我們可以讓預測的偏差變大,以換取更穩定的預測
- Shrinkage
- 改善預測的準確度時,很常使用的技巧
Regularization
- 在迴歸的範例中,我們尋找的是最小方差直線
- 我們要找到參數\(\beta_0, \beta_1, ...\) 來最小化: \[(y - \beta_0 - \beta_1 x_1 - \beta_2 x_2 - ...)^2\]
- Regularization
- 「評分」的算式加上對參數的控制,讓預測更穩定(但是偏差也因此變大)
- 我們要找到參數\(\beta_0, \beta_1, ...\) 來最小化: \[(y - \beta_0 - \beta_1 x_1 - \beta_2 x_2 - ...)^2 + \lambda (\left\Vert \beta_1 \right\Vert + \left\Vert \beta_2 \right\Vert + ...)\]
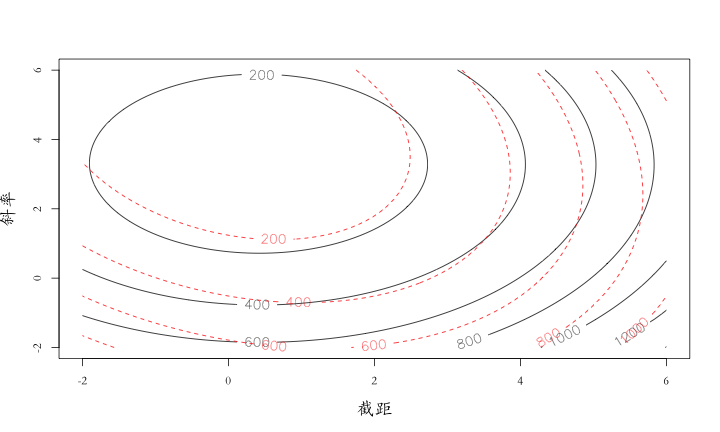
範例:高維線性模型
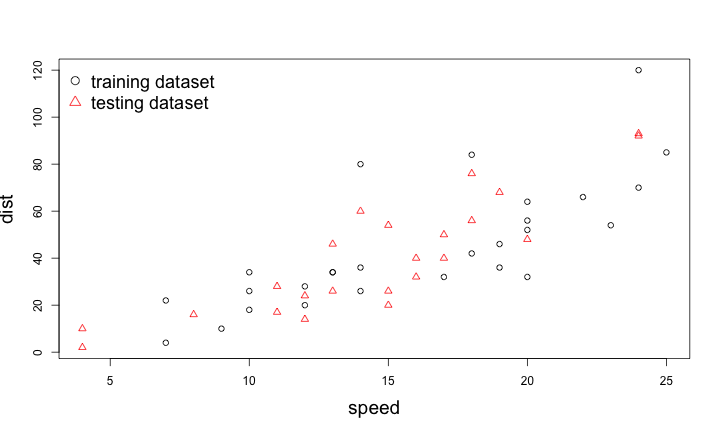
範例:高維線性模型
\[dist = \beta_0 + \beta_1 speed + \beta_2 speed^2 + \beta_3 speed^3\]
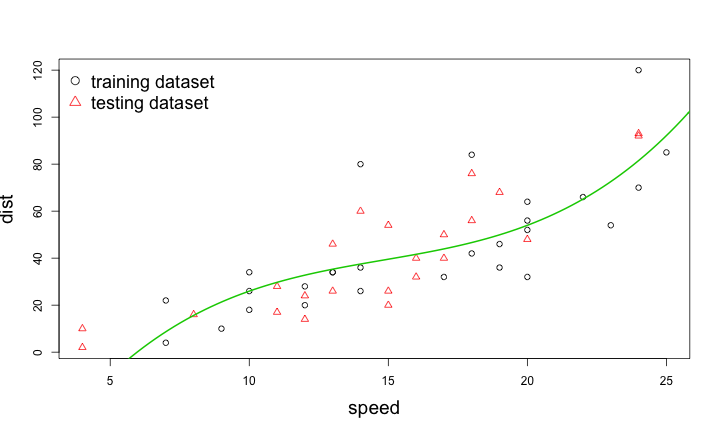
範例:高維線性模型與Regularization
\[dist = \beta_0 + \beta_1 speed + \beta_2 speed^2 + \beta_3 speed^3 + 10 (\beta_1^2 + \beta_2^2 + \beta_3^2)\]
Training Loss
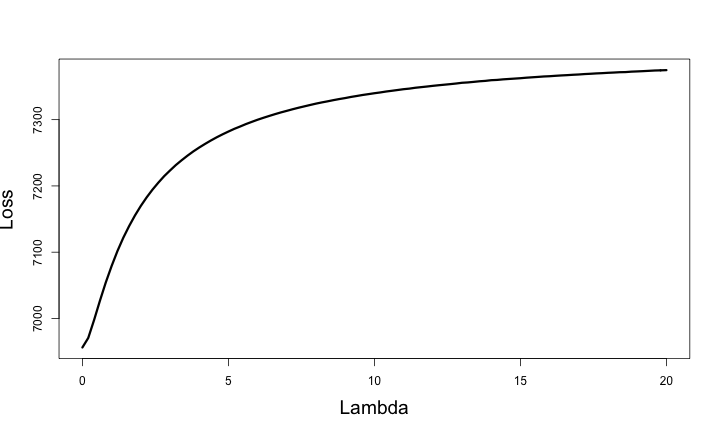
Testing Loss

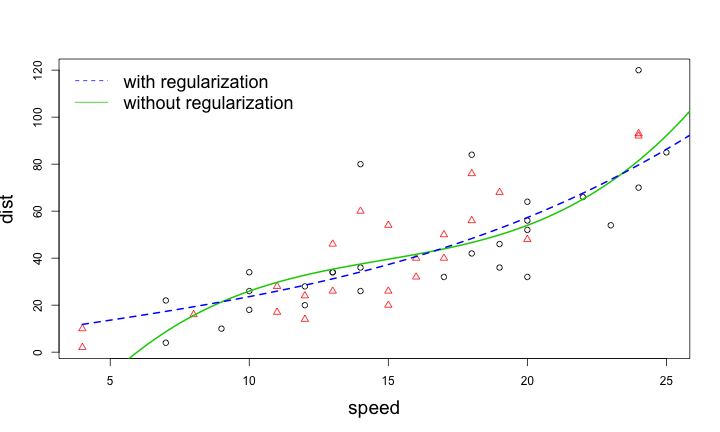
Regularization 的特點
- 大部分狀況,可以提昇模型的準確度
- 提昇模型的穩定性
- 降低優化的難度
- \(L_0\) Regularization 可以用於挑選重要的解釋變數
- 資料需要標準化
- 多了一個(或多個)需要調整的參數
R套件介紹: glmnet
- 請同學完成
Optional-RMachineLearning-03-Regularization
Support Vector Machine
空間移轉與次元刀
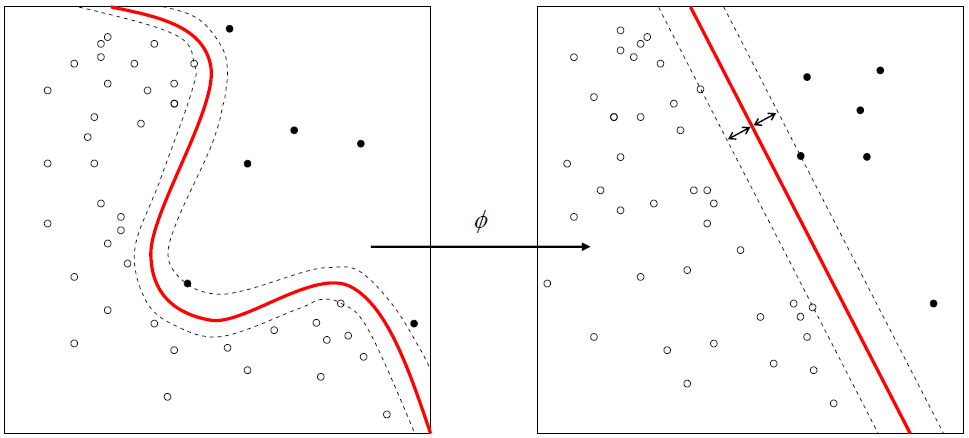
空間移轉與次元刀
比較一般的線性模型與SVM Regression
- 線性模型:
\[l(y, f(x) = (y - f(x))^2\]
- SVM:
\[l(y, f(x)) = \left\{\begin{array}{lc} 0 & \text{ if } \left\lVert y - f(x) \right\rVert < \varepsilon \\ \left\lVert y - f(x) \right\rVert - \varepsilon & \text{ otherwise } \end{array}\right.\]
比較一般的線性模型與SVM Regression
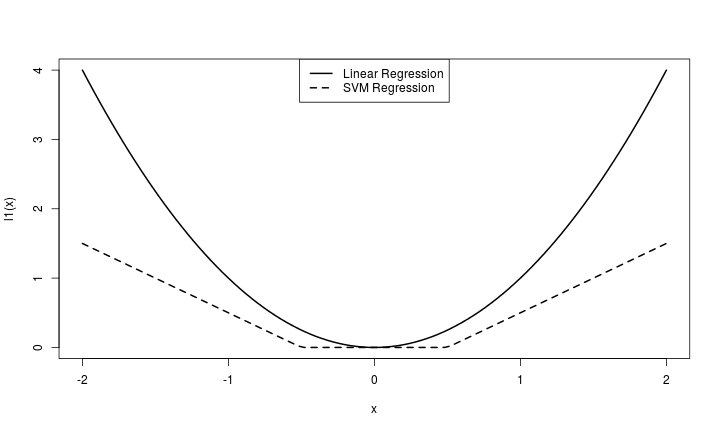
比較一般的線性模型與SVM Regression
R套件介紹:e1071
- 請同學完成
Optional-RMachineLearning-04-Support-Vector-Machine
Decision Tree
Decision Tree
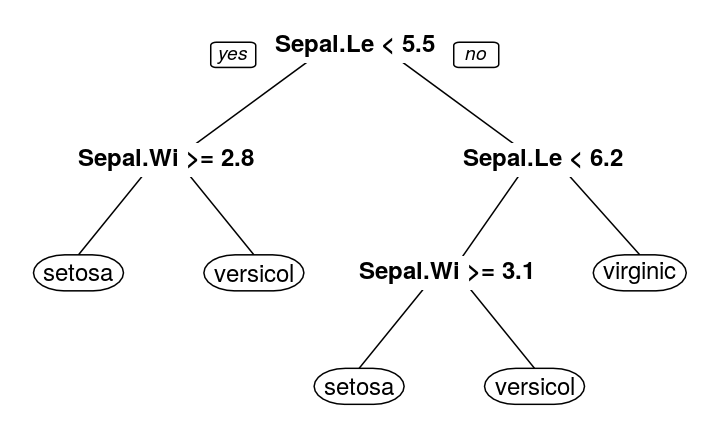
如何長出一顆決策樹?
- 一次一次長一個分支
- 計算分數,每次都挑讓分數變得最好的分支長法
- 當長不下去時,停止
- https://youtu.be/eKD5gxPPeY0?t=3m48s
Decision Tree

R 套件介紹:rpart
- 請同學完成
Optional-RMachineLearning-05-Decision-Tree
Bagging 與 Random Forest
Bagging: 眾人的智慧
- 如果我們有很多「不太準的模型」,能不能讓它們一起工作,變得更準?
- 一起工作的方法:
- 表決(分類問題)
- 取平均(迴歸問題
Random Forest
- 每次隨機抽出部份的「解釋變數」(而不是資料)
- 利用這些抽出的解釋變數長出一棵決策樹(不太準的模型)
- 長出大量的決策樹後進行投票(眾人的智慧)
Random Forest
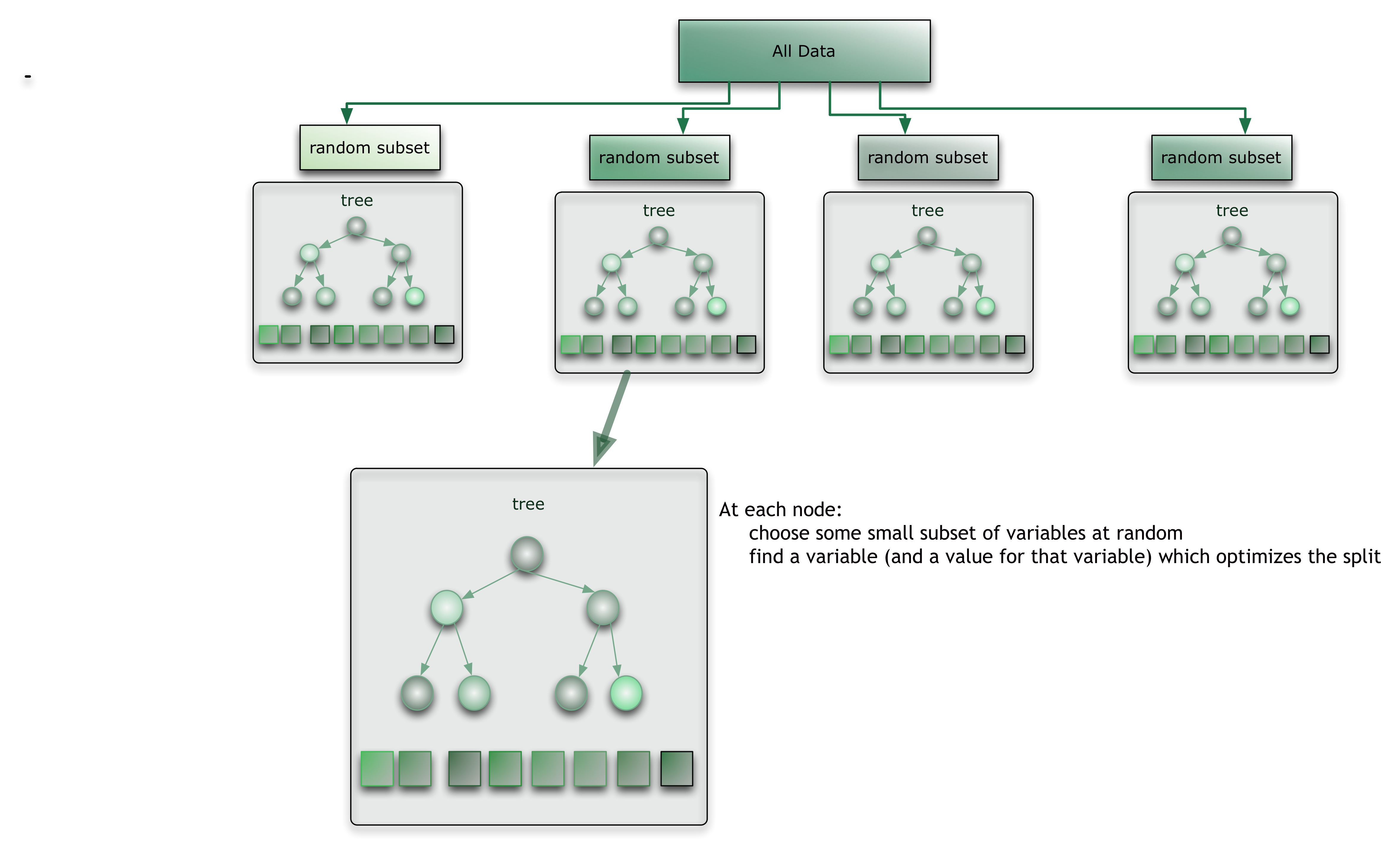
https://citizennet.com/blog/2012/11/10/random-forests-ensembles-and-performance-metrics/
Random Forest
- 非線性
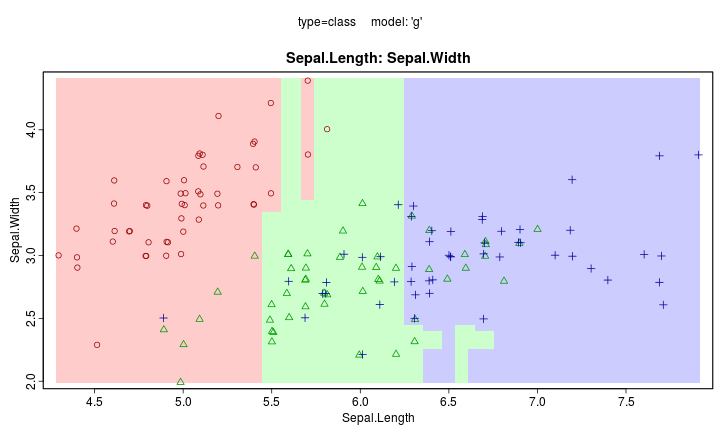
R套件:randomForest
Boosting 與 GDBT
Boosting
- 從錯誤中學習:
- 在training dataset上學習
- 驗證學習的成果,挑出做的不好的題目
- 重新學一遍,但是更針對原先做不好的題目
- 將學習的軌跡加權後做整合
- \[F_{m+1} = F_m + h\]
Boosting
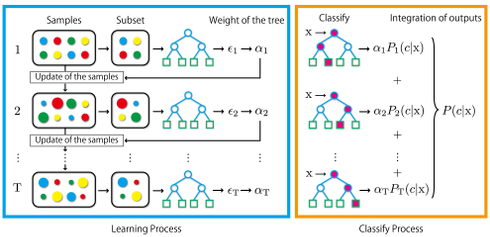
Gradient Boosting
- 將模型視為是在training dataset所產生的space
- \((F(x_1), F(x_2), ...F(x_N))\)
Gradient Boosting Decision Tree
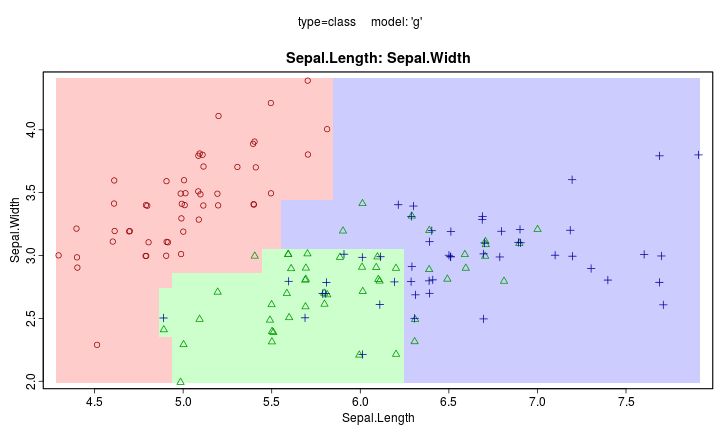
R套件介紹:xgboost
- 嶄露頭角: https://www.kaggle.com/c/higgs-boson
- 冠軍: https://www.kaggle.com/c/tradeshift-text-classification/forums/t/10901/solution-sharing
- 請同學完成:
Optional-RMachineLearning-06-Gradient-Boosted-Decision-Tree
Neuron Network
Neuron
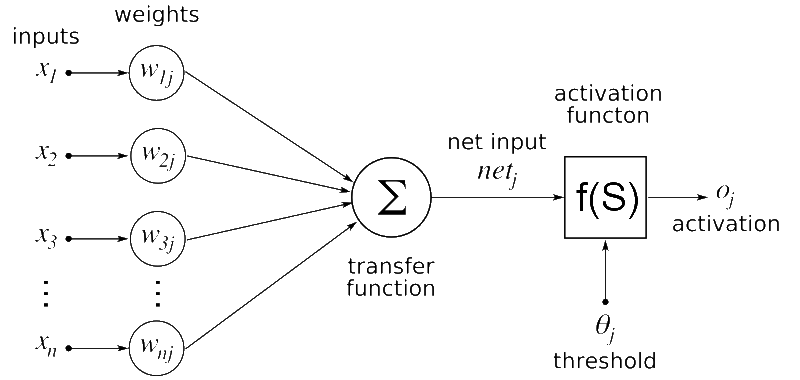
Artificial Neuron
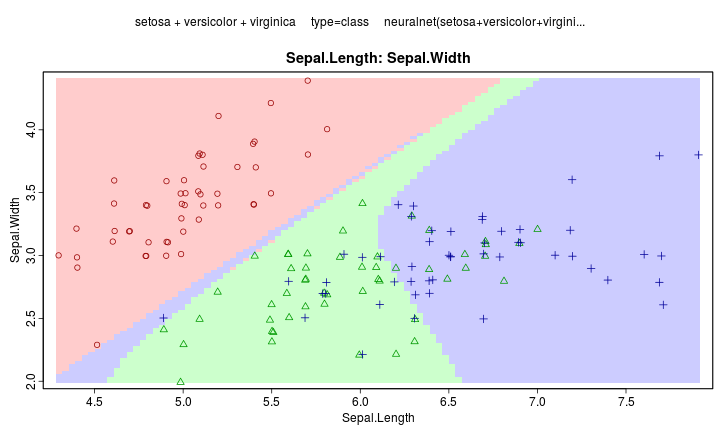
Neuron Network
- 串聯許多神經元
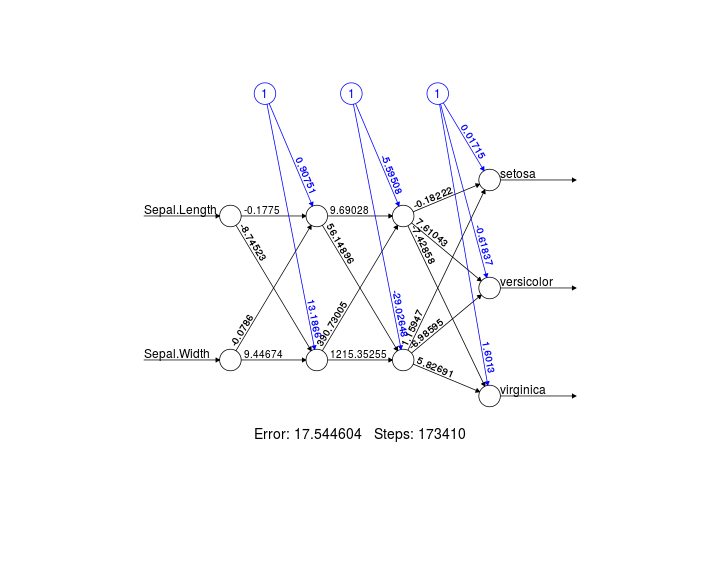

Neuron Network Online Demo
Neuron Network
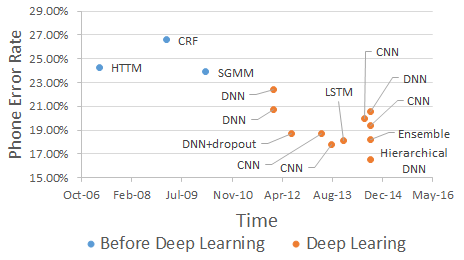
Deep Learning
- 簡單的看法: 深層的Neuron Network
- 近年的發展: Autoencoder, word2vec, Restricted Boltzmann machine, Dropout, Convolution Neuron Network, ...
語音辨識
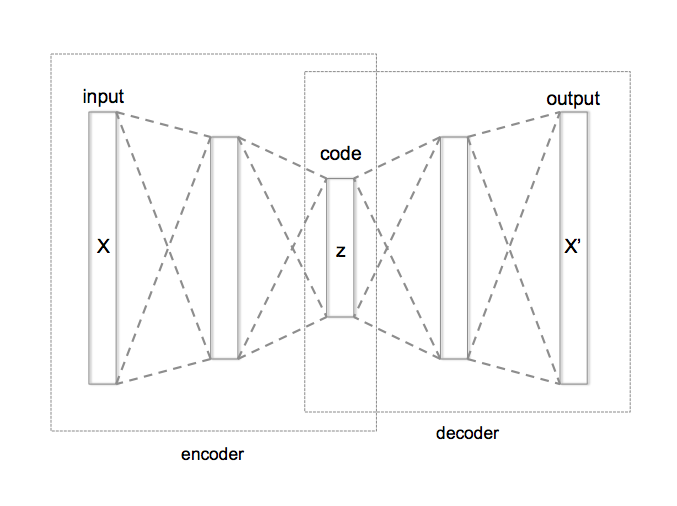
Autoencoder
- 用途: 降維 $X$,找出潛在的結構(我們會在下一週討論到)
Word2vec (結構學習)
- 輸入大量的文本,利用Neuron Network解決兩個問題:
- 用兩邊的字預測中間的字
- 用中間的字預測兩邊的字
- 每個字可編碼成 \(\mathbb{R}^d\) 的向量
- 字之間的距離可以看成同義字
- 巴黎 - 法國 + 義大利 = 羅馬
- 語意搜尋功能的入門
Deep Learning 常見誤解
Deep Learning 比較好是因為它比較複雜?
- 同樣的多的Neurons
- 1層
- 高層
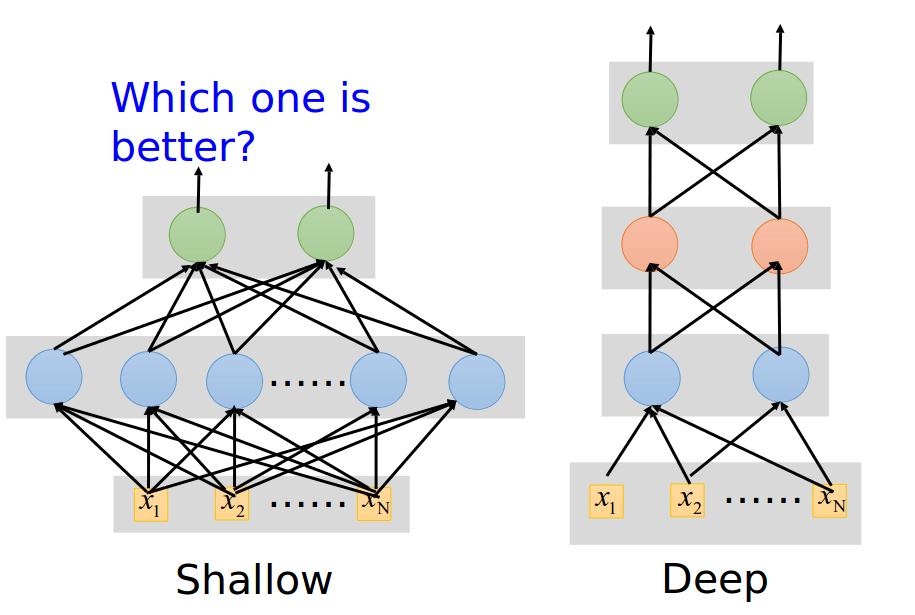
Deep Learning 比較好是因為它比較複雜?
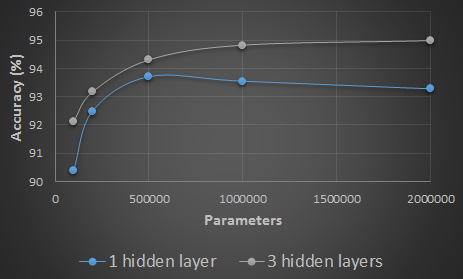
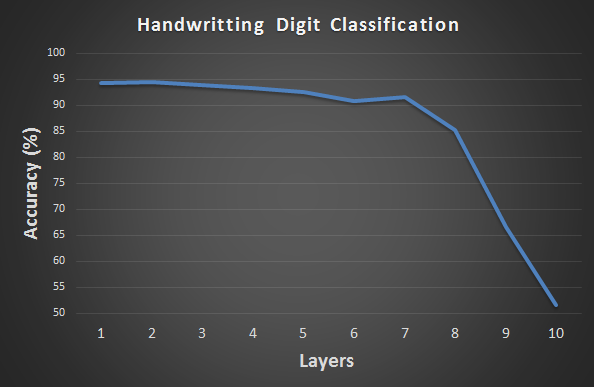
Deep Learning 越多層就越好?
Neuron Newtork 的實作
- R 上目前做的比較好的,可能是 mxnet
- 目前還沒有Windows的版本
- 請轉職Python
機器模型與實務
真實的資料是活的
- Offline \(\neq\) Online
- 線下指標無法取代實際指標
- 線下實驗 ==> 線上實驗 ==> 產品(系統化)
不是無限制的追求準確度
- 線性模型:準確度90% 一個工程師,4 hr / week
- 深度學習:準確度99% 一個工程師團隊加上研究者 full-time
實務的機器學習挑戰還有其他限制
- 機器資源有限
- 工程師的時間有限
- 預測的時間有限
- 模型的大小有限
- 系統的維護有成本
如何從實務問題變成機器學習問題
- 機器學習問題:分類與迴歸
- 實務問題:價值
我要賺錢
決定實作機器學習之前
- 重要的三個問題(Google):
- 資料哪裡來?
- 資料怎麼處理?
- 資料怎麼變現?